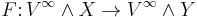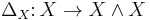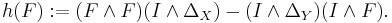Hopf invariant
In mathematics, in particular in algebraic topology, the Hopf invariant is a homotopy invariant of certain maps between spheres.
Contents |
Motivation
In 1931 Heinz Hopf used Clifford parallels to construct the Hopf map
 ,
,
and proved that 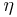 is essential, i.e. not homotopic to the constant map, by using the linking number (=1) of the circles
is essential, i.e. not homotopic to the constant map, by using the linking number (=1) of the circles
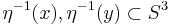 for any
for any  .
.
It was later shown that the homotopy group 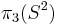 is the infinite cyclic group generated by
is the infinite cyclic group generated by 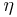 . In 1951, Jean-Pierre Serre proved that the rational homotopy groups
. In 1951, Jean-Pierre Serre proved that the rational homotopy groups
for an odd-dimensional sphere ( odd) are zero unless i = 0 or n. However, for an even-dimensional sphere (n even), there is one more bit of infinite cyclic homotopy in degree
odd) are zero unless i = 0 or n. However, for an even-dimensional sphere (n even), there is one more bit of infinite cyclic homotopy in degree 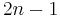 . There is an interesting way of seeing this:
. There is an interesting way of seeing this:
Definition
Let 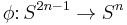 be a continuous map (assume
be a continuous map (assume 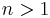 ). Then we can form the cell complex
). Then we can form the cell complex
where 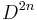 is a
is a 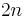 -dimensional disc attached to
-dimensional disc attached to 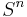 via
via  . The cellular chain groups
. The cellular chain groups 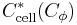 are just freely generated on the
are just freely generated on the  -cells in degree
-cells in degree  , so they are
, so they are  in degree 0,
in degree 0,  and
and 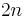 and zero everywhere else. Cellular (co-)homology is the (co-)homology of this chain complex, and since all boundary homomorphisms must be zero (recall that
and zero everywhere else. Cellular (co-)homology is the (co-)homology of this chain complex, and since all boundary homomorphisms must be zero (recall that 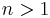 ), the cohomology is
), the cohomology is
Denote the generators of the cohomology groups by
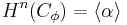 and
and 
For dimensional reasons, all cup-products between those classes must be trivial apart from  . Thus, as a ring, the cohomology is
. Thus, as a ring, the cohomology is
The integer 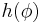 is the Hopf invariant of the map
is the Hopf invariant of the map  .
.
Properties
Theorem: 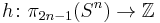 is a homomorphism. Moreover, if
is a homomorphism. Moreover, if  is even,
is even,  maps onto
maps onto 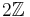 .
.
The Hopf invariant is 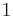 for the Hopf maps (where
for the Hopf maps (where  , corresponding to the real division algebras
, corresponding to the real division algebras 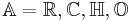 , respectively, and to the double cover
, respectively, and to the double cover 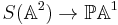 sending a direction on the sphere to the subspace it spans). It is a theorem, proved first by Frank Adams and subsequently by Michael Atiyah with methods of K-theory, that these are the only maps with Hopf invariant 1.
sending a direction on the sphere to the subspace it spans). It is a theorem, proved first by Frank Adams and subsequently by Michael Atiyah with methods of K-theory, that these are the only maps with Hopf invariant 1.
Generalisations for stable maps
A very general notion of the Hopf invariant can be defined, but it requires a certain amount of homotopy theoretic groundwork:
Let  denote a vector space and
denote a vector space and 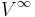 its one-point compactification, i.e.
its one-point compactification, i.e. 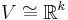 and
and
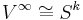 for some
for some  .
.
If 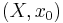 is any pointed space (as it is implicitly in the previous section), and if we take the point at infinity to be the basepoint of
is any pointed space (as it is implicitly in the previous section), and if we take the point at infinity to be the basepoint of 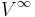 , then we can form the wedge products
, then we can form the wedge products
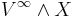 .
.
Now let
be a stable map, i.e. stable under the reduced suspension functor. The (stable) geometric Hopf invariant of  is
is
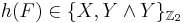 ,
,
an element of the stable 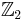 -equivariant homotopy group of maps from
-equivariant homotopy group of maps from  to
to 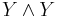 . Here "stable" means "stable under suspension", i.e. the direct limit over
. Here "stable" means "stable under suspension", i.e. the direct limit over  (or
(or  , if you will) of the ordinary, equivariant homotopy groups; and the
, if you will) of the ordinary, equivariant homotopy groups; and the 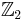 -action is the trivial action on
-action is the trivial action on  and the flipping of the two factors on
and the flipping of the two factors on 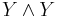 . If we let
. If we let
denote the canonical diagonal map and  the identity, then the Hopf invariant is defined by the following:
the identity, then the Hopf invariant is defined by the following:
This map is initially a map from
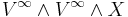 to
to 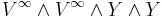 ,
,
but under the direct limit it becomes the advertised element of the stable homotopy  -equivariant group of maps. There exists also an unstable version of the Hopf invariant
-equivariant group of maps. There exists also an unstable version of the Hopf invariant  , for which one must keep track of the vector space
, for which one must keep track of the vector space  .
.
References
- Adams, J.F. (1960), "On the non-existence of elements of Hopf invariant one", Ann. Math. (The Annals of Mathematics, Vol. 72, No. 1) 72 (1): 20–104, doi:10.2307/1970147, JSTOR 1970147
- Adams, J.F.; Atiyah, M.F. (1966), "K-Theory and the Hopf Invariant", The Quarterly Journal of Mathematics 17 (1): 31–38, doi:10.1093/qmath/17.1.31
- Crabb, M.; Ranicki, A. (2006), The geometric Hopf invariant, http://www.maths.ed.ac.uk/~aar/slides/hopfbeam.pdf
- Hopf, Heinz (1931), "Über die Abbildungen der dreidimensionalen Sphäre auf die Kugelfläche", Mathematische Annalen 104: 637–665, doi:10.1007/BF01457962, ISSN 0025-5831
- Shokurov, A.V. (2001), "Hopf invariant", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=h/h048000

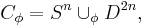
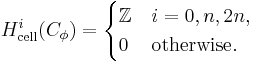
![H^*(C_\phi) = \mathbb{Z}[\alpha,\beta]/\langle \beta\smile\beta = \alpha\smile\beta = 0, \alpha\smile\alpha=h(\phi)\beta\rangle.](/2012-wikipedia_en_all_nopic_01_2012/I/3c17cb2367981bb84928226220c3f9b3.png)